African Research Journal of Education and Social Sciences, 5(2), 2018
Authors: Faith Kathure Mberia and Boniface Njuguna Mwangi
Africa Nazarene University, P.O. Box 53067 – 00200, Nairobi
Email of the Corresponding Author: bmwangi@anu.ac.ke
Abstract: Mathematical English is a unique language based on ordinary English, with highly stylized formal symbol systems. Owing to the fact that it has its own lexicon, syntax, semantics and literature; this makes it more difficult to understand than ordinary English. Understanding abstract mathematics concepts is challenging to students at different levels in Kenya. This study sought to investigate the influence of mathematical English on the performance of class 8 learners in Miriga Mieru West Division, Imenti North Sub – County Meru County. The study `objectives were: to investigate the influence of vocabulary, syntactical features and lexical ambiguities on learners’ mathematics performance. The study was guided by Meaney’s model of mathematics register acquisition. It used correlational research design. The target population for this study was class 8 learners in public primary schools. The study comprised of 30 public primary schools, 1080 class 8 learners and 36 class 8 mathematics teachers. The study used random sampling to select the schools and learners while purposive sampling was used to select teachers from the sampled schools. Data was obtained using Learners’ Mathematics Test Questionnaire (LMTQ) and Trained Mathematics Teacher’s Questionnaire (TMTQ). The study established that the three independent variables statistically significantly influenced mathematics performance for class 8 learners. Syntactical features had the greatest influence on performance (β = 4.549; t = 3.506, p < 0.05). This was closely followed by lexical ambiguity (β = 4.173; t = 5.103, p < 0.05). Vocabulary had the least influence (β = 3.383; t = 2.928, p ˂ 0.05). The study therefore concluded that vocabulary, lexical ambiguity and syntactical features are critical components in primary school mathematics that a learner should understand in order to perform well. The study recommended that teachers should among other things guide learners on how to interpret mathematical vocabulary and comprehend mathematical language in teaching and learning process.
Keywords: Mathematical English, Syntactical Features, Lexical Ambiguities, School English Performance
1. INTRODUCTION
Mathematics is crucial not only for success in school, but also in producing informed citizens, productive in their careers and in their personal endeavors. In today’s technology – driven society, demands are placed on individuals to be able to interpret and use mathematics to make sense of information in diverse situations. The study of mathematics equips students with knowledge, skills and practice that are crucial for successful and gratifying participation in society Ministry of Education Canada, (2005).
Learning mathematics results in more than mastery of basic skills: it equips students with a concise and powerful means of communication. Mathematical structures, operations, processes and language provide students with a structure and tools for analysis and expressing ideas clearly. Through mathematics activities that are practical and relevant to their lives, students develop insight, problem – solving skills, and related technological skills that they can apply in their daily lives and eventually in the work place Ministry of Education Canada, (2005).
The development of any nation depends upon her scientific and technological advancement built on a sound mathematical education of making the citizens successfully functional in the natural and applied sciences. The study of mathematics therefore goes a long way to equip students to live effectively in our modern age of science and technology (NPE, 2004). Despite the important role that mathematics plays in society there has always been poor performance in the area at national examinations in Kenya Aduba, (2003).
The resounding question of the 1980’s, extending over to the 1990s is “why are the literates from schools so mathematically illiterate?” this question which confronts the serious thinkers of mathematics today is not limited to any one country, any one culture or for that matter any one system of education; it is being raised almost universally (Morris & Arora, 1992). Studies conducted by American Institute for Research (AIR, 2007) to investigate mathematics performance in USA students – 4th and 8th grades as compared with their peers around the world and another by (National Assessment of Education Progress [NAEP]) assessed the progress in mathematics of student’s in grade 4, 8 and 12. The results showed that grade 4 pupils performed below the average mark consistently from 1996 – 2007.
In Kenya, poor performance in mathematics at Kenya Certificate of Primary Education (KCPE) has been and still is a subject of much debate among politicians, teachers, parents, educational specialists and other stakeholders (Elizabeth, 2013). In the year 2005, 671, 417 pupils sat for K.C.P.E exam in Kenya and the mathematics raw mean was 53.94%, while in the year 2007, 698, 364 pupils did the exam and obtained a percentage raw mean of 49.24 (Ministry of Education, 2010). These poor results calls for urgent need in determining the causes of poor performance and offering effective solution if Kenya is to achieve scientific and technological advancements.
Specifically, Miriga Mieru West Division, Imenti North sub-county Meru County has been posting dismal mean marks in mathematics as depicted in Table 1.
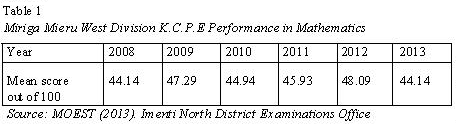
Table 1 shows the performance in mathematics in a span of six years. It is evident that the performance has been persistently low taking into account that the national mean score stands at 58. Dismal performance in mathematics has over the years attracted many researchers. However, while most of researchers have dwelt on teaching methods and approaches, availability of teaching resources, mathematics teacher demographics such as academic qualification and teaching experience (Kamau, 2010), (Nyamongo, Sang, Nyaoga & Matoke, 2014); (Yala & Wanjohi, 2011), very few have engaged in the effect of mathematical English on pupils performance. Mathematical English can be a major hindrance to performance in mathematics. This study endeavored to investigate the influence of mathematical English on class eight learners’ performance in mathematics in public primary schools in Miriga Mieru West Division, Imenti North sub county Meru County, Kenya.
2. REVIEW OF RELATED LITERATURE
Mathematics is not ‘language free’ and due to its particular vocabulary, syntax and discourse it can cause problems for students learning it in a second language (Barton & Neville-Barton, 2005). (Gough, 2007) believes that mathematics is more than a language. (Latu, 2005) points out that students need to be strong in both their general and mathematical language. It is further argued in the same study, that if learners’ mathematical background is weak, then it does not matter what language they are taught or tested in because they will have a problem with their mathematics. (Gough, 2007) holds that problems in mathematics are experienced when specialized words are in conflict with the everyday understanding. Of a similar opinion are (Gorgorio & Planas, 2001) who also found out that students had difficulties understanding everyday words within mathematical context. (Krawec & Sweeney, 2008) point out that mathematics language is highly technical with specific vocabulary connected to content.
A study done in Eldoret Municipality showed that learners had problems interpreting the meanings of mathematical technical terms correctly. In this study for instance, students were tested on the mathematical vocabulary ‘odd’, most learners gave the term ‘uneven’ to explain the meaning of odd. The response ‘uneven’ suggested that the students interpreted the example in terms of the number that not even which is not meaningful in the mathematical sense Edna (2014). A study done in Tharaka Nithi County showed that majority of the students had problems solving numbers with mathematics vocabulary. For instance a number containing the mathematical vocabulary ‘singular matrix’ seemed to complicate learners’ understanding in the word problem. This problem posed challenges because the word singular has different meaning in ordinary English and takes a specific meaning in mathematics (Mercy, 2015).
(Biemiller, 2001) has shown that there is a strong relationship between vocabulary knowledge and the overall academic achievement in school, this is particularly true with mathematics. (Thompson and Rubestein, 2000) say that students must understand mathematics vocabulary if they are to master content and be able to apply it in future situations. According to (Marzano, 2004) standardized test scores could be positively influenced by as much as 33% if teaching academic vocabulary is done. This is echoed by (Clifford and Gore 2008) who found out that under-performing mathematics students who received instruction gained by as much as 93% in standardized test. Whereas students may do well in computation their ability to apply mathematics skills may be impended if they do not understand the vocabulary utilized in instruction and word problems.
Syntax in Mathematics is the arrangement, order and appearance of words and phrases in mathematics word problems. The syntactic feature that causes most confusion for students is word order. In most cases the written and symbolic forms of an operation are written in different orders. For example “take 3 from 8 and the difference between 8 and 3 are both written as 8 – 3” (Newman, 1983; Abedi & Lord, 2001). Students tend to solve such a problem by subtracting the larger number from the smaller number, regardless of the order in which they are presented leading to reversal errors. Abedi & Lord (2001) point out that students face more difficulty when word order is important in some situations and not in others. For example “3 multiplied by 7 can also be written as 3 times 7 or 7 times 3”.
The syntactical complexity of statements and questions posed in mathematics may be challenging to the learners. For example “which number between 25 and 30 cannot be divided equally by either 2 or 3?” for a student to solve such a problem they must bear in mind several pieces of detailed information and also relate these together in the precise way implied by the complex syntax of the sentence. Such a task is very challenging, but it is very common to primary school pupils doing mathematics (Haylock & Thangata, 2007). Foong (2009) says that students’ failure to solve word problems was not due to their lack of arithmetic ability but their inability to construct an appropriate problem representation as a result of the way the problem was constructed.
Abedi and Lord (2001) noted that many mathematical problems are presented in passive and abstract forms. For example “the difference in the ages of two students is six years” . The same statement could be expressed in a simpler form by saying “Sandra is six years older than Peter”. Word order is affected by passive voice. For example when the passive form of “a sample of 25 was selected” is converted to the active form it will be, “ he selected a sample of 25”, the order of the noun and verb ‘sample’ and ‘selected’ respectively is reversed. Students face greater challenges interpreting mathematical texts in passive voice and abstract forms (Abedi & Lord, 2001). The study found out that such syntactical complexities contributed to low performance in mathematics.In line with this is Neville – Barton & Barton (2005) who found out that students whom English is a second language have a disadvantage approximated to be between 10 & 15 percent in mathematics as a result of language difficulties. Language feature found to be sources of difficulty were word order and prepositions which had the most significant causations.
Lexical Ambiguity is a word or phrase that has more than one meaning. Similarly it is the presence of two or more possible meanings within a single word or phrase. When words that are not part of everyday English are used differently in a domain, such words are said to have lexical ambiguity. Moschkovic (2007) describes learning mathematics in a second language as twofold because it includes mathematical concepts to be learnt and learning and comprehending mathematical meanings of words.This is because there are words extracted from the ordinary English language yet used to describe the mathematical concept that is only seen in mathematical situation. Kieffer and Lesaux (2010) point out that unfamiliar words is one of the challenge that create barriers to content area texts. There may be difficulties for students with mathematical terms that have multiple meanings.
Jorgensen and Dole (2011) identified three types of lexical ambiguity which include homonyms, homophones and polysemy. Homonyms are words that look and sound the same but have different meanings. Confusion to students come when they hear one meaning but the teacher is intending the term to be interpreted in another way. For example, “what is the length of time between 9.05 a.m and 9.55a.m?” “How do students make sense of this type of question when they have a construct of length as a unit of measure that can be measured with a ruler? (Jorgensen & Dole, 2011).
Homophones are words with different spellings but sound the same for example two halves make a whole. The students may be hearing two halves make a hole. The learners could be left wondering what the teacher is talking about. Polysemy is a word that has two or more different but related meanings for example product, base. In mathematics the word product means multiplication but in the daily usage the word means something that has been produced as a process or is manufactured. Durkin and Shire (1991) have noted that mathematics is not devoid of such ambiguities. Sternberg (2003) points out that understanding mathematics discourse does not rest exclusively on the interpretation of words written in textbooks and spoken by the teacher but also the knowledge of the physical, social and cultural contexts within which the discourse takes place. From the study findings of the Mediterranean journal of social sciences (2014), it showed that there was a significant relationship between lexical ambiguities in algebra and grade 9 academic performances. The findings suggest that the lexical ambiguity in algebra does determine grade 9 students’ academic performance. The study however covered only one topic on algebra. The current study covered different topics in order to establish whether lexical ambiguity influences academic performance.
3. METHODOLOGY
The study adopted a correlational research design. The researcher was interested in knowing whether there would be relationships between the independent variables and the dependent variable without necessarily manipulating the independent variables. The dependent variable, which was learners’ mathematics performance, was paired with the independent variables (Mathematical English) to know both their joint and relative predictive values. The target population was 1,080 class 8 learners, 36 mathematics teachers from the 30 public schools in Miriga Mieru West division. Class 8 was considered for the study since in the past several years mathematics K.C.P.E results of Miriga Mieru West Division were below average. It was also assumed that class eight will have covered the primary school mathematics syllabus. For this study, a sample of 50% of schools and teachers was considered. This is because the schools and teachers are a small population and at the same time for better representation. Therefore, 15 schools and 18 teachers were selected. As pointed out by Gay (1992), 10% is a representative sample for a large population. This study sampled 10% of the 1080 learners which was 108 learners.
Schools were selected through random sampling while mathematics teachers were purposively selected since the study targeted only trained mathematics teachers. The study targeted class eight learners from public primary schools where 108 learners were selected at random. Learners’ data were collected using the Learners’ Mathematics Test Questionnaire (LMTQ). This was basically three separate achievement tests focused on mathematics vocabulary, syntactical features and lexical ambiguities in mathematics. Most of the test items were adapted from previous K.C.P.E test papers. Data was also collected from teachers through the Trained Mathematics Teachers’ Questionnaire (TMTQ). In this questionnaire, teachers views on the challenges encountered by students in solving mathematical questions inclined to vocabulary, syntactical features and lexical ambiguities in mathematics was sought. In addition the past performance of their students in a standard mathematics examination was sought. The standard examination was a full paper of 50 questions akin to KCPE paper and in which questions involving vocabulary, syntactical features and lexical ambiguities were included
4. RESULTS
In order to achieve the three objectives and test the study’s three hypotheses, the results from the three tests from the Learners’ Mathematics Test Questionnaire were regressed on the scores attained in the standard examination. All the four tests were scored out of 100. The study aimed at assessing the composite and relative contributions of the three components of mathematical English considered in this study to learners’ overall academic performance in mathematics. Tables 2, 3 and 4 depict the summary of multiple regression analysis.

According to Table 2, the multiple correlation coefficients R had a value of 0.835. Multiple R is the correlation between the observed values of dependent variable and the value of dependent variable predicted by the multiple regression models. Therefore, the large value of R (0.835) meant there was a large or strong positive correlation between the predicted and observed values of the level of implementation of creative activities curriculum. As such, multiple R is a gauge of how well the model predicts the observed data.
The coefficient of determination R2 which is the proportion of variance in the dependent variable that can be explained by the independent variables was found to be 0.792 implying that 79.2 % of variance in the performance in mathematics was explained by score in vocabulary, syntactical and lexical ambiguity related questions. Further, the adjusted R2 value of 0.774 means that 77.4 % of variance in mathematics performance in a standard paper could be accounted for if the model has been derived from the population from which the sample was taken.
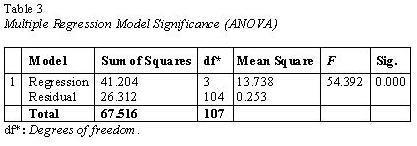
Table 3 shows the analysis of variance (ANOVA) output. The F-ratio in the ANOVA table tests whether the overall regression model is a good fit for the data. That is, the ANOVA shows whether the model, overall, results in a significantly good degree of prediction of the outcome variable. The table shows that the joint independent variables statistically significantly predict the dependent variable, F (3, 104) = 54.392, p <0.05 and that other variables not included in this model may have accounted for the remaining variance. In other words, the regression model was a good fit for the data.
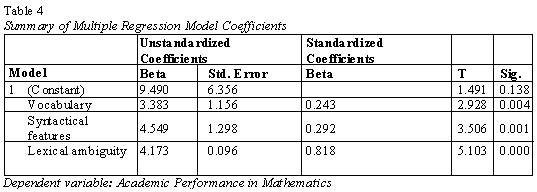
Table 4 reveals the relative contribution of the three independent variables to the dependent variable, expressed as beta weights. The regression model capturing the hypothesized relationship was as follows: Y= β0+ β 1×1+β2×2+ β3×3+ε, where y = predicted performance in mathematics, x1 = Average score on vocabulary, x2 = Average score on syntactical features, x3 = Average score on lexical ambiguity, while ε is the error term. Assuming the error term ε to be zero and substituting the unstandardized coefficients β values, the estimated multiple regression equation becomes: y = 9.490 + 3.383x1 +4.549x2+4.173x3.
According to the regression equation established, taking all factors constant at Zero, the level of performance in mathematics was 9.490. The constant βo value of 9.490 shows that if all the investigated predictors were assumed not to have significant influence, the performance in mathematics would be influenced by a factor of 9.490 by other predictors. The β values indicate the individual contribution of each predictor to the model if the effects of all other predictors are held constant. In other words, the β values show the relationship between performance in mathematics and each predictor. Therefore, holding other factors constant, an improvement in vocabulary will improve the performance in mathematics by 3.38 units, while an improvement in syntax will improve performance in mathematics with 4.55 units similarly an improvement in lexical ambiguity will improve performance with 4.2 units.
In order to have a direct evaluation and better understanding into significance of predictors, the standardized β values that do not depend on the units of measurement of variables, are used. The standardized β values give the figure of standard deviations that the effect will vary as a result of one standard deviation change in the predictor. Consequently, the above table shows that all the independent variables had a positive impact on the performance of mathematics. This shows that if more practice by the pupils on the independent variables, that is, on vocabulary, syntax features and lexical ambiguity could lead to an improvement in the overall performance of mathematics. Table 4.36 indicates that syntactical features had the most influence on mathematics performance (β = 4.549; t = 3.506, p < 0.05) followed by lexical ambiguity β = 4.173; t = 5.103, p < 0.05 and vocabulary was the least influencer β = 3.383; t = 2.928, p < 0.05.
In order to test the study’s three formulated hypotheses (section 1.2), the t statistic that tests whether a B value is significantly different from zero (H0: β =o) is considered (refer to Table 4). Table 4 shows that syntactical features had the greatest and statistically significant influence on mathematics overall performance (β = 4.549; t = 3.506, p < 0.05). Thus the first null hypothesis was rejected. Similarly, performance in lexical ambiguity (β = 4.173; t = 5.103, p < 0.05) and vocabulary (β = 3.383; t = 2.928, p < 0.05) had a significant influence. Consequently the two hypotheses H02 and H03 were also rejected.
5. DISCUSSION
The role of mathematics vocabulary cannot be over emphasized because its acquisition and comprehension is the foundation to all other important mathematical activities. It was established in this study that knowledge of mathematical vocabulary had a significant positive influence on mathematics performance (β = 3.383, p < 0.05). These findings are in line with those of Benson (2015) whose study findings revealed a positive relationship between students’ scores in knowledge of mathematical vocabulary and mathematics performance. This implies that a good mastery of mathematics vocabulary improves mathematics, for this to happen, teachers should define these words in a precise manner if learners are to benefit from instruction. Marzano (2004) points out that standardized test scores could be positively influenced by as much as 33% if teaching academic vocabulary is done. Shanahan and Shanahan (2003) pointed out that mathematics vocabulary is unique in that many words have both general and specific meaning, while at the same time key terms should be defined in a precise manner. Some words may be unfamiliar to students, while others have common meanings that are different from their usage in mathematical contexts. Mathematics curriculum materials may contain new words that represent new concepts and while such vocabulary have limited application beyond the specific mathematical contexts in which they are taught, those new words represent new knowledge students must build to understand key concepts (Harper & de Jong 2004).
The findings of this study are in agreement with that of Meaney (2005), who found out that ‘borrowed’ words from everyday English cause significance problems to many learners. The non – mathematical meanings of these terms can influence mathematical understanding as well as being a source of confusion. Barwell, (2005) found out that to properly solve mathematical word problems, students need to develop deeper and wider vocabulary knowledge. Further still evidence from several scholars Qian, (1998, 1999, and 2002); Qian & Schedl (2004) and Shiotsu & Weir (2007) showed that vocabulary knowledge is essential for the comprehension of texts.
This study revealed that majority of the teachers interviewed (83.3%) were of the opinion that English language was an impediment to learning mathematics. In line with these findings are those of Manyara (2012) which indicated that 86.7% of teachers interviewed agreed that that students’ English ability influenced their performance. The research further showed that although teachers were comfortable teaching mathematics concepts in English their students had difficulties communicating mathematically. A study done in Tharaka Nithi also revealed that majority of learners had problems solving numbers with mathematical vocabulary (Mercy 2015). The researcher feels that teachers and all relevant stakeholders should find ways of accommodating such deficiencies for learning to be meaningful.
This study showed that syntactical features had a significant positive influence on mathematics performance (β = 4.549; p < 0.05). This therefore means an improvement in performance in questions involving syntactical features will improve the overall mathematics performance. When comparing the frequency and percentage of learners with correct solutions, a higher percentage of students performed better in mathematics vocabulary than word problems containing syntactic features. This low performance implies that syntax of word problems appeared to cause problems for learners. The findings of this study are in agreement with findings of Neville – Barton and Barton (2005) who found out that syntax posed greater difficulty than vocabulary in word problems. Qian (1999) found out that greater syntactical knowledge leads to successful comprehension, which is an important step in solving mathematics.
Even when learners know the vocabulary and computation required, the organization of words prevents them from fully understanding the problem (Leach & Bowling, 2000). Martiniello (2006) also supports the findings of this study relating to syntax. Evidence from her study findings state that difficulties in mathematics were associated with syntactical features. Long phrases, prepositional nouns or a noun phase led to difficulty in understanding. Neville – Barton & Barton (2005) advance that word order and prepositions were language features that were the greatest sources of difficulty for learners whom English is the second language. Wheeler and Mcnutt (2001) also support the findings of this study where they found out that syntactical complexity of mathematics word problems created difficulty in solving, although the word problems were within learners’ reading and vocabulary levels.
Lexical ambiguity in mathematics also had a significant and positive influence on mathematics performance (β = 4.173; t = 5.103, p < 0.05). Therefore it can be concluded that for learners to perform well in mathematics a lot of improvement needs to be done in this area. Mediterranean journal of social sciences (2014), concur with findings of this study. The study showed a significant relationship between lexical ambiguity and mathematics performance.
According to Martiniello (2009), polysemous words were among linguistic features that hinder learners from solving mathematics problems. While lexical ambiguity is recognized as “an essential characteristic of the conceptual development of the subject and as a feature which opens the door to new ideas, new insights and deeper understanding, teachers should deliberately define every term as used in mathematics without any assumption. Homonyms as noted by Zevenbergen (2001) are an aspect of mathematics but are a source of confusion to learners especially when explicit explanation is not given. A surprising finding was that even though students comprehend the overall meanings of word problems in this area of lexical ambiguity a good number of respondents demonstrated poor conceptual understanding on a few of them. Even when only symbols were used a good number of respondents were not able to give correct answers.
6. CONCLUSION AND RECOMMENDATIONS
Mathematics vocabulary has a positive significant influence on mathematics performance. This therefore, means that an improvement in learners’ mathematical vocabulary will lead to better performance in mathematics. Without teachers’ explicit explanation of mathematics vocabulary, learners may not understand a topic or anything related to the said topic (Wilhem 2007). For academic achievement to be attained, learners must understand the meaning of words instead of just hearing them.
This study also found that syntactical features statistically and significantly influences mathematics performance. This therefore means that an improvement in understanding of syntactical features will improve mathematics performance significantly. Likewise the study showed that lexical ambiguity has a significant effect on mathematics performance. This shows that mathematics performance is not statistically independent and therefore an improvement in lexical ambiguity improves mathematics performance.
The study found that vocabulary influences mathematics performance. It is imperative that teachers deliberately teach learners how to interpret vocabulary and comprehend mathematical language. The teacher can use the everyday meaning of mathematical words to simplify the specialized mathematical words. Code switching may also be used where the teacher shares the first language with learners. Use of well-designed language programs can be used to improve student’ understanding in mathematics. The teacher should make an effort to define the technical terms without any assumptions.
The study revealed that syntactical features do influence mathematics performance. Teachers are therefore advised to use modeling and scaffolding. A teacher can rephrase a learner’s response given in everyday language into more appropriate mathematical language. Teachers should use active voice as opposed to passive voice in framing the question. Shorter sentences should be used instead of lengthy ones which confuse learners. The teacher should use appropriate mathematical language and create time within the lesson where learners can communicate mathematically. Peer tutoring should be encouraged within the mathematics and positive reinforcement given to correct responses. As much as possible the teacher should encourage students to verbalize all the mathematics tasks given in order to acquire the content-specific language.
Lexical ambiguity also showed a positive influence on mathematics performance. Teachers must therefore teach learners through good mathematical English. Collaboration between mathematics and English teachers should be encouraged. This is because mathematical English and ordinary English do not function separately, instead learners and teachers should interweave them for effective mathematical learning. Teachers should use teaching and learning aids and where possible involve learners to manipulate them. Simplified English should be used in order to accommodate learners’ varied needs since they use English as a second language.
REFERENCES
Abedi, J., & Lord, C. (2001). The language factor in mathematics tests. Applied Measurement in
Education, 14, (3), 219 – 234.
Adler, T. (1997). A participatory inquiry approach and mediation of mathematical knowledge in
Multilingual classrooms. Educational Studies in Mathematics, 235-258.
Aduba, D. (2003). Kenya Certificate of Secondary Education, examination results released by
Minister of education. Daily Nation, Nairobi: Nation Media Group.
Barton, B., & Neville-Barton, P. (2003). Language issues in undergraduate mathematics’ a report
of two studies. New Zealand Journal of mathematics.
Barwell, R. (2005). Ambiguity in the Mathematics Classroom. Language and Education 19, (2),
118 – 126.
Biermiller, A. (2001). Teaching vocabulary: Early, direct, sequential. The American Educator.
25, (1), 24 – 28.
Durkin, K., & Shire, B. (1991). Lexical ambiguity in mathematics contexts.
Elizabeth, R. (2013). Teacher commitment and mathematics performance in primary school: A
meeting point
Foong, P. Y. (2009). Review of research on mathematical problem solving in Singapore in W.K
Yoong L.P Yee, B. Kaur, F.P. . Yel and S.N, Fong (Eds). Mathematics education: The
Singapore Journey, 263 – 297 . Singapore. World scientific.
Gay L.R. (1992). Education Research: Competencies for analysis and application. New
York: Macmillan.
Gough, J. (2007). Conceptual complexity and apparent contradictions in mathematics
language. Australian Mathematics Teacher, 63, (2), 8 – 15.
Gorgorio, N., & Planas, N. (2001). Teaching mathematics in multilingual classrooms.
Educational studies in mathematics, 47, (1), 7 – 33.
Jorgensen, R., & Dole, S. (2011). Teaching mathematics in primary schools (2nd Ed.).
International design by Book house Sydney.
K. Durkin & B. Shire (Eds.). Language in mathematics education: Research and practice (pp. 71 – 84). Milton Keynes: Open University Press.
Kamau, B. (2010). Impact of pre-school progress on mathematics performance in lower primary schools of Makuyu zone, Murang’a south district, Kenya (Unpublished M. Ed project).
University of Nairobi.
Kieffer, M. J., & Lesaux, N. K. (2010). Morphing into adolescent; active word learning for English – language learners and their classmates in middle school. Journal of Adolescent & Adult Literacy, 54, (1), 47 – 56.
Manyara, S. M. (2012). Influence of students’ English language competence on performance in secondary schools in Meru Central District, Meru County. Unpublished thesis Nairobi University.
Marzano, R. J. (2004). Building background knowledge for academic achievement: Research on what works in schools. Alexandria VA: Association for Supervision and curriculum Development.
Meaney, T. (2006). Mathematics Registers. Acquisition set, (3), 39 – 43.
Mediterranean journal of social sciences. (2014). Lexical ambiguity in Algebra, method of Instruction as determinant of Grade 9 students’ academic performance in East London District. MCSER Publishing, Rome – Italy.
Ministry of Education, Canada. (2005). The Ontario curriculum grades 1-8, mathematics. Retrieved from http://www ‘edu. Gov.on.ca.
Ministry of Education Science and Technology. (2001). Teaching and learning primary mathematics module Nairobi: MOEST Nairobi.
Ministry of education Science and Technology (2010). Teaching and learning primary mathematics. Mathematics module, MOEST Nairobi.
Morris, R., & Arora, M. S. (1992). Studies in mathematics education moving into the twenty –first century. Paris: UNESCO.
Moschkovich, J. N. (2002). A situated and social cultural perspective on bilingual mathematics learners. Mathematics Thinking and Learning, 4, (2&3), 189 – 212.
Newman, A. (1983). Language and mathematics. Sydney: Harcourt, Brace & Jovanovich.
Nyamongo, D. N., Sang, A., Nyaoga, R. B., & Matoke, Y. K. (2014). Relationship between school based factors and students’ performance in kenya certificate of secondary examination, in Masaba North District, Kenya. International Journal of Education and Research, 2(10), 129-144.
Shiotsu, T., & Weir, C. J. (2007). The relative significance of syntactic knowledge and vocabulary breadth in the prediction of reading comprehension test performance. Language Testing, 24, (1), 99 – 128.
Yala, P. O., & Wanjohi, W. C. (2011). Performance determinants of KCSE in mathematics in secondary schools in Nyamira Division, Kenya. Asian Social Science, 7(20): 107-112.
Wilhelm, J. D. (2007). Imagining a new kind of self: Academic language, identify and content area learning. Voices from the Middle, 15, (1), 44 – 45.
Zevenbergen, R. (2001). Mathematical literacy in the middle years. Literacy learning, 9(2), 21 – 28.

